Теория игр. Как мыслить стратегически

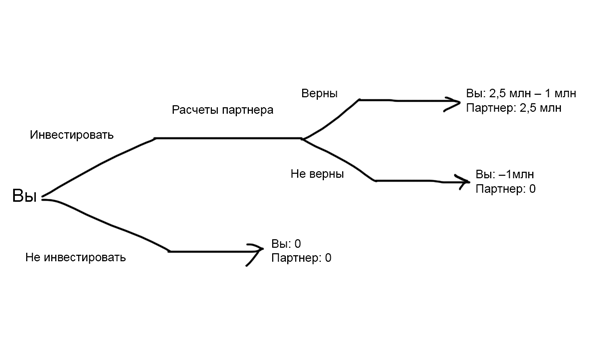
Теория игр — область математики, которая помогает принимать стратегически верные решения. По этой теории практически каждая ситуация, которая заставляет вас делать выбор, считается игрой. Иногда один игрок побеждает за счет выигрыша другого, иногда проигрывают или выигрывают оба. Теория игр учит мыслить стратегически, с точки зрения математики, чтобы повысить шансы на победу.
Сегодняшний выпуск о книге «Теория игр», в которой ученые-экономисты Авинаш Диксит и Барри Нэлбафф описывают методы стратегического мышления. Эти методы помогают принимать взвешенные решения в работе, спорте и личной жизни.
 Барри Нэлбафф |
 Авинаш Диксит |
Обычно во введении к рассылке я пишу, кому особенно полезен выпуск. Сегодня мне нечего сказать, потому что уметь мыслить стратегически полезно всем.
|
|
|
|
Автор: Люда Сарычева
Источник: https://bigplans.megaplan.ru/theory-of-games
 |
Теория игр — область математики, которая помогает принимать стратегически верные решения. По этой теории практически каждая ситуация, которая заставляет вас делать выбор, считается игрой. Иногда один игрок побеждает за счет выигрыша другого, иногда проигрывают или выигрывают оба. Теория игр учит мыслить стратегически, с точки зрения математики, чтобы повысить шансы на победу. |
РэдЛайн, создание сайта, заказать сайт, разработка сайтов, реклама в Интернете, продвижение, маркетинговые исследования, дизайн студия, веб дизайн, раскрутка сайта, создать сайт компании, сделать сайт, создание сайтов, изготовление сайта, обслуживание сайтов, изготовление сайтов, заказать интернет сайт, создать сайт, изготовить сайт, разработка сайта, web студия, создание веб сайта, поддержка сайта, сайт на заказ, сопровождение сайта, дизайн сайта, сайт под ключ, заказ сайта, реклама сайта, хостинг, регистрация доменов, хабаровск, краснодар, москва, комсомольск |
|
Теория игр — область математики, которая помогает принимать стратегически верные решения. По этой теории практически каждая ситуация, которая заставляет вас делать выбор, считается игрой. Иногда один игрок побеждает за счет выигрыша другого, иногда проигрывают или выигрывают оба. Теория игр учит мыслить стратегически, с точки зрения математики, чтобы повысить шансы на победу. |
РэдЛайн, создание сайта, заказать сайт, разработка сайтов, реклама в Интернете, продвижение, маркетинговые исследования, дизайн студия, веб дизайн, раскрутка сайта, создать сайт компании, сделать сайт, создание сайтов, изготовление сайта, обслуживание сайтов, изготовление сайтов, заказать интернет сайт, создать сайт, изготовить сайт, разработка сайта, web студия, создание веб сайта, поддержка сайта, сайт на заказ, сопровождение сайта, дизайн сайта, сайт под ключ, заказ сайта, реклама сайта, хостинг, регистрация доменов, хабаровск, краснодар, москва, комсомольск |

Дайджест новых статей по интернет-маркетингу на ваш email
Новые статьи и публикации
- 2024-09-30 » Как быстро запустить Laravel на Windows
- 2024-09-25 » Next.js
- 2024-09-05 » OpenAI рассказал, как запретить ChatGPT использовать содержимое сайта для обучения
- 2024-08-28 » Чек-лист: как увеличить конверсию интернет-магазина на примере спортпита
- 2024-08-01 » WebSocket
- 2024-07-26 » Интеграция с Яндекс Еда
- 2024-07-26 » Интеграция с Эквайринг
- 2024-07-26 » Интеграция с СДЕК
- 2024-07-26 » Интеграция с Битрикс-24
- 2024-07-26 » Интеграция с Travelline
- 2024-07-26 » Интеграция с Iiko
- 2024-07-26 » Интеграция с Delivery Club
- 2024-07-26 » Интеграция с CRM
- 2024-07-26 » Интеграция с 1C-Бухгалтерия
- 2024-07-24 » Что такое сторителлинг: техники и примеры
- 2024-07-17 » Ошибка 404: что это такое и как ее использовать для бизнеса
- 2024-07-03 » Размещайте прайс-листы на FarPost.ru и продавайте товары быстро и выгодно
- 2024-07-01 » Профилирование кода в PHP
- 2024-06-28 » Изучаем ABC/XYZ-анализ: что это такое и какие решения с помощью него принимают
- 2024-06-17 » Зачем вам знать потребности клиента
- 2024-06-11 » Что нового в работе Яндекс Метрики: полный обзор обновления
- 2024-06-11 » Поведенческие факторы ранжирования в Яндексе
- 2024-06-11 » Скорость загрузки сайта: почему это важно и как влияет на ранжирование
- 2024-05-27 » Подборка сервисов для расшифровки аудио в текст
- 2024-05-27 » PostgreSQL 16. Изоляция транзакций. Часть 2
- 2024-05-06 » Как настраивать конверсионные стратегии: работа над ошибками
- 2024-04-22 » Комментирование кода и генерация документации в PHP
- 2024-04-22 » SEO в России и на Западе: в чем основные отличия
- 2024-04-22 » SEO для международного масштабирования
- 2024-04-22 » Как использовать XML-карты для продвижения сайта
Бог тянет за одну руку, а черт - за обе ноги Буш Вильгельм - (1832-1908) - немецкий поэт и художник |
Мы создаем сайты, которые работают! Профессионально обслуживаем и продвигаем их !
Как мы работаем
Заявка
Позвоните или оставьте заявку на сайте.
Консультация
Обсуждаем что именно Вам нужно и помогаем определить как это лучше сделать!
Договор
Заключаем договор на оказание услуг, в котором прописаны условия и обязанности обеих сторон.
Выполнение работ
Непосредственно оказание требующихся услуг и работ по вашему заданию.
Поддержка
Сдача выполненых работ, последующие корректировки и поддержка при необходимости.
















 Мы создаем практически любые сайты от продающих страниц до сложных, высоконагруженных и нестандартных веб приложений! Наши сайты это надежные маркетинговые инструменты для успеха Вашего бизнеса и увеличения вашей прибыли! Мы делаем красивые и максимально эффектные сайты по доступным ценам уже много лет!
Мы создаем практически любые сайты от продающих страниц до сложных, высоконагруженных и нестандартных веб приложений! Наши сайты это надежные маркетинговые инструменты для успеха Вашего бизнеса и увеличения вашей прибыли! Мы делаем красивые и максимально эффектные сайты по доступным ценам уже много лет! Комплексный подход это не просто продвижение сайта, это целый комплекс мероприятий, который определяется целями и задачами поставленными перед сайтом и организацией, которая за этим стоит. Время однобоких методов в продвижении сайтов уже прошло, конкуренция слишком высока, чтобы была возможность расслабиться и получать \ удерживать клиентов из Интернета, просто сделав сайт и не занимаясь им...
Комплексный подход это не просто продвижение сайта, это целый комплекс мероприятий, который определяется целями и задачами поставленными перед сайтом и организацией, которая за этим стоит. Время однобоких методов в продвижении сайтов уже прошло, конкуренция слишком высока, чтобы была возможность расслабиться и получать \ удерживать клиентов из Интернета, просто сделав сайт и не занимаясь им...
 Мы оказываем полный комплекс услуг по сопровождению сайта: информационному и техническому обслуживанию и развитию Интернет сайтов.
Мы оказываем полный комплекс услуг по сопровождению сайта: информационному и техническому обслуживанию и развитию Интернет сайтов.

 Контекстная реклама - это эффективный инструмент в интернет маркетинге, целью которого является увеличение продаж. Главный плюс контекстной рекламы заключается в том, что она работает избирательно.
Контекстная реклама - это эффективный инструмент в интернет маркетинге, целью которого является увеличение продаж. Главный плюс контекстной рекламы заключается в том, что она работает избирательно.